|
Engineering Computational Technology
Edited by: B.H.V. Topping and Z. Bittnar
A. Meyer
Faculty of Mathematics, Technical University of Chemnitz, Germany
Keywords: finite elements, adaptive work, preconditioned conjugate gradient.
We look for efficient implementations of adaptive finite element simulations
for problems in mechanics and physics. Here, efficient means both with
respect to memory requirements and with respect to time.
The first wish ``low memory'' requires data structures which allow quick
execution of the main tasks
- mesh handling (refinement/coarsening)
- forming (element) matrix / right hand side
- solving the linear systems
- post processing / error estimation [1,4] /
error control for mesh refinement
by storing as less information as possible. The second wish ``short running
times'' require such data structures with
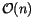 effort for all the main
tasks sketched above,
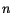when  is the number of nodes (actually in one mesh of the
adaptive series).
In our experiments we have defined three data structures:
| ``nodes'': |
containing coordinates and solution values of each node |
| ``edges'': |
containing 3 nodes and refinement information to son-edges |
| |
or geometry/boundary conditions of finest edges, resp. |
| ``elements'': |
containing its edges and nodes, material information |
| |
and the element matrix and right hand side |
For completing a finite element calculation on these data structures, we have
to incorporate special projection procedures for handling ``hanging nodes'',
(a necessary tool for most simple refinement ideas) and for all kinds of
restrictions from boundary conditions.
We give a special variant of the well-known Preconditioned Conjugate Gradient
Method running in a subspace of
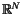 , which is defined from a special
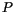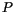projection  . Then we describe the structure of the projector for
solving these problems for linear and qudratic elements:
- In case of hanging nodes, calculate a solution that belongs to the
conformal subspace (continuous function).
- Satisfy boundary restrictions for some boundary nodes.
We give an example of a Signorini contact simulation [3,2], where all these
projections are included. Here, the solve up to
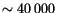 nodes requires
near the same running time as one linear elastic problem with prescribed
displacements.
-
- 1
- M. Ainsworth, J. Oden,
A Posteriori Error Estimation in Finite Element Analysis,
Comp.Meth.Appl.Mech.Eng. 142(1997)1-2, 1-88.
- 2
- J.Schöberl,
Solving the Signorini problem on the basis of
domain decomposition techniques,
Computiong 60 (1993), 323-344.
- 3
- A. Signorini,
Sopra akune questioni di elastistatica,
Attil della Societa Italiana per il Progresso
delle Scienzie (1993).
- 4
- R. Verfürth,
A Review of a
posteriori Error Estimation and Adaptive Mesh Refinement
Techniques,
Wiley-Teubner, Chichester, Stuttgart (1996).
return to the contents page
|
