|
Progress in Engineering Computational Technology
Edited by: B.H.V. Topping and C.A. Mota Soares
F. Suerich-Gulick*, C.Y. Lepage+ and W.G. Habashi*+
*Department of Mechanical Engineering, McGill University, Montreal, Canada
+Newmerical Technologies International, Montreal, Canada
Keywords: computational fluid dynamics, mesh adaptation, anisotropy, unstructured meshes, turbulence models, boundary layer flow.
In the work presented here, a mesh adaptation module is extended to account for
the requirements of turbulence models on 3-D unstructured tetrahedral meshes.  adaptation is implemented by modifying the error metric of near-wall elements to
obtain an appropriate grid point distribution in the boundary layer. In the final paper,
results will be presented to demonstrate the improvements in the meshes that result
from this new function and the corresponding improvements in the CFD solutions.
adaptation is implemented by modifying the error metric of near-wall elements to
obtain an appropriate grid point distribution in the boundary layer. In the final paper,
results will be presented to demonstrate the improvements in the meshes that result
from this new function and the corresponding improvements in the CFD solutions.
Most turbulence models require that the distribution of grid points in the
boundary layer fall within a specific range of  values. To achieve this, values. To achieve this,  adaptation is incorporated into the standard mesh adaptation process to adjust the
thickness of elements in the near-wall region. The need for and importance of
adaptation is incorporated into the standard mesh adaptation process to adjust the
thickness of elements in the near-wall region. The need for and importance of  adaptation has been documented in recent literature [1,2,3].
adaptation has been documented in recent literature [1,2,3].
Many turbulence models require that near-wall elements be orthogonal to the
wall, necessitating the use of hexahedral meshes or hybrid tetrahedral meshes with
layers of prisms on the walls.  adaptation on these types of meshes has already
been implemented [1]. Alternately, certain turbulence models such as
Spalart-Allmaras may be used with entirely unstructured tetrahedral meshes. This can be
advantageous when dealing with complex geometries that often present challenges
for generating semi-structured meshes. Therefore, adaptation on these types of meshes has already
been implemented [1]. Alternately, certain turbulence models such as
Spalart-Allmaras may be used with entirely unstructured tetrahedral meshes. This can be
advantageous when dealing with complex geometries that often present challenges
for generating semi-structured meshes. Therefore,  adaptation for tetrahedral
meshes is implemented to facilitate the generation of initial meshes and improve the
quality of the solutions obtained following adaptation. adaptation for tetrahedral
meshes is implemented to facilitate the generation of initial meshes and improve the
quality of the solutions obtained following adaptation.
It should be noted that the capacity to produce anisotropic meshes is particularly
important in this case, because the turbulence model requires an extremely high
mesh density in the direction normal to the wall. The adaptation software produces
elements that are stretched in the directions parallel to the wall, so the adapted mesh
has a much smaller number of nodes than an equivalent isotropic mesh with the
same boundary layer resolution. However, adapting these stretched elements
presents additional difficulties, especially for 3-D meshes.
The standard mesh adaptation process is governed by the error metric, in the form
of a Hessian matrix H, which is computed from the second derivatives of the
adaptation scalar.  adaptation for tetrahedral meshes is implemented by modifying
the error metric in the near-wall regions and then proceeding with the adaptation in
the entire domain in the standard fashion. A similar approach for 2-D meshes has
been documented in the literature [3,4]. adaptation for tetrahedral meshes is implemented by modifying
the error metric in the near-wall regions and then proceeding with the adaptation in
the entire domain in the standard fashion. A similar approach for 2-D meshes has
been documented in the literature [3,4].
In order to modify the metric in the direction normal to the no-slip wall, the
Hessian is decomposed into its eigenvectors such that
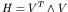 , and the
eigenvectors are rotated so that one of them points in the normal direction. The
eigenvalue , and the
eigenvectors are rotated so that one of them points in the normal direction. The
eigenvalue
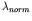 corresponding to the normal eigenvector is then set to corresponding to the normal eigenvector is then set to  to
achieve the local element thickness to
achieve the local element thickness  . The thickness at a distance . The thickness at a distance 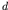 from the wall is
computed using the target element thickness from the wall is
computed using the target element thickness  at the wall and the growth ratio at the wall and the growth ratio 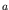 set
by the user: set
by the user:
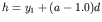 . .
For  adaptation, adaptation,  is calculated from the is calculated from the  value in the solution and the target value in the solution and the target
 set by the user. For mesh smoothing without a solution, set by the user. For mesh smoothing without a solution,  is set directly by the
user. The distance is set directly by the
user. The distance 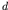 to the no-slip walls is computed everywhere in the domain by
solving a Poisson equation. The normal to the nearest no-slip wall is approximated
by the gradient of the wall distance scalar. to the no-slip walls is computed everywhere in the domain by
solving a Poisson equation. The normal to the nearest no-slip wall is approximated
by the gradient of the wall distance scalar.
 adaptation for unstructured 3-D tetrahedral meshes allows users to produce
high-quality anisotropic meshes for turbulent solutions without the difficulties of
generating structured meshes for complex geometries. The initial mesh obtained
from the mesh generation software may be first smoothed to increase the density in
the boundary layer for the initial solution and then adapted with a target adaptation for unstructured 3-D tetrahedral meshes allows users to produce
high-quality anisotropic meshes for turbulent solutions without the difficulties of
generating structured meshes for complex geometries. The initial mesh obtained
from the mesh generation software may be first smoothed to increase the density in
the boundary layer for the initial solution and then adapted with a target  value to
obtain the optimal mesh for turbulent solutions. value to
obtain the optimal mesh for turbulent solutions.
-
- 1
- C.Y. Lepage, F. Suerich-Gulick, and W.G. Habashi, Anisotropic 3-D Mesh
Adaptation on Unstructured Hybrid Meshes, AIAA Paper 2002-0859, 2002.
- 2
- A. Khawaja, T. Minyard, and Y. Kallinderis, Adaptive Hybrid Grid Methods,
Comput. Methods Appl. Mech. Eng., 189, 1231-1245, 2002.
- 3
- G. Xia, D. Li, and C.L. Merkle, Anisotropic Grid Adaptation on Unstructured
Meshes, AIAA Paper 2001-0443, 2001.
- 4
- M.J. Castro-Diaz, F. Hecht, B. Mohammadi, and O. Pironneau, Anisotropic
Unstructured Mesh Adaptation for Flow Simulations, Int. J. Numer. Meth.
Fluids, 25, 475-491, 1997.
return to the contents page
|
