Progress in Engineering Computational Technology
Edited by: B.H.V. Topping and C.A. Mota Soares

Chapter 5

Resolution of Sparse Linear Systems of Equations: the RPK Strategy

G. Montero, R. Montenegro, J.M. Escobar and E. Rodríguez
Institute of Intelligent Systems and Numerical Applications in Engineering, University of Las Palmas de Gran Canaria, Spain

Keywords: sparse linear systems of equations, iterative solvers, Krylov subspace methods, preconditioning, reordering.

An over view of advanced techniques for solving large sparse linear systems of equations is presented. We are interested in the resolution of,

where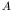

is a sparse, large and non-singular matrix. The first question is if it is better a direct or an iterative resolution. The main disadvantage of direct methods compared with iterative ones is that the rounding errors are accumulated along the process of direct solving. Besides they require more memory requirements due to the fill-in effect. On the other hand, in non steady problems where there must be solved many similar systems of equations, iterative solvers may use the solution obtained in the previous time step as initial guess. So, nowadays it is preferred to use iterative methods in front of direct ones for large scale sparse linear systems of equations.

The reordering techniques based on graph theory, that were initially applied in the resolution by using direct methods, provide matrices with smaller band width or a sparsity pattern with a lower number of nonzero inner entries. However, this reduction may be used in order to improve the effect of incomplete factorisation preconditioners on the rate of convergence of iterative methods. The effect several reordering techniques on different Krylov subspace methods may be seen in [1,2,3,4,5].

Preconditioning techniques improve the convergence of iterative methods. Here, we study some standard preconditioners, in particular, Jacobi, SSOR, ILU and sparse approximate inverse.

On the other hand, some Krylov subspace methods for solving linear systems of equations are considered. For symmetric problems, the Conjugate Gradient method is proposed [6]. However, for non-symmetric linear systems there exist several alternatives that may be classified into three family of methods: orthogonalisation, biorthogonalisation and normal equation methods (see [7,8]). Among orthogonalisation methods for nonsymmetric linear systems that apply the Arnoldi algorithm [9], we study the Generalised Minimum Residual method (GMRES) [10]. On the other hand, we study the Biconjugate Gradient Stabilised method (Bi-CGSTAB) [11] and its quasi-minimal residual variant, the QMRCGSTAB algorithm [12]. Besides, we consider the use of the Least-square QR method (LSQR) [13] based on the normal equation.

References

1

M. Benzi, D.B. Szyld, A. van Duin, "Orderings for incomplete factorization preconditioning of nonsymmetric problems", SIAM J. Sci. Comput., 20, 5, 1652-1670, 1999.

2

M. Benzi, M. Tuma," Orderings for factorized sparse approximate inverse preconditioners", SIAM J. Sci. Comput., 30, 5, 1851-1868,2000.

3

L.C. Dutto, "The Effect of Ordering on Preconditioned GMRES Algorithm", Int. Jour. Num, Meth. Eng., 36, 457-497, 1993.

4

E. Flórez, M.D. García, L. González, G. Montero, "The effect of orderings on sparse approximate inverse preconditioners for non-symmetric problems", Adv. Engng. Software, 33, 7-10, 611-619, 2002.

5

G. Montero, M. Galán, P. Cuesta, G. Winter, "Effects of stochastic ordering on preconditioned GMRES algorithm", in B.H.V. Topping & M. Papadrakakis eds., Advances in Structural Optimization, 241-246, Civil-Comp Press, Edinburgh, 1994.

6

M.R. Hestenes, E. Stiefel, "Methods of Conjugate Gradients for Solving Linear Systems", Jour. Res. Nat. Bur. Sta., 49, 6, 409-436, 1952.

7

G. Montero, G. Winter, A. Suárez, M. Galán, D. García, "Contribution to Iterative Methods for Nonsymmetric Linear Systems: GMRES, BCG and QMR Type Methods", in Computational Methods and Neural Networks. Part Two: Computational Methods, M. Sambandhamy & M.P. Bekakos, Eds., Dynamic Publishers, Inc., 97-128, 1999.

8

N.M. Nachttigal, S.C. Reddy, L.N. Trefethen, "How Fast Are Nonsymmetric Matrix Iterations?", SIAM J. Matr. Anal. Appl., 13, 3, 796-825, 1992.

9

W.E. Arnoldi, "The Principle of Minimized Iteration in the Solution of the Matrix Eingenvalue Problem", Quart. Appl. Math., 9, 17-29, 1951.

10

Y. Saad, M. Schultz, "GMRES: A Generalized Minimal Residual Algorithm for Solving Nonsymmetric Linear Systems", SIAM J. Sci. Statist. Comput., 7, 856-869, 1986.

11

H.A. van der Vorst, "Bi-CGSTAB: A Fast and Smoothly Converging Variant of Bi-CG for the Solution of Nonsymmetric Linear Systems", SIAM J. Sci. Comput., 13, 631-644, 1992.

12

T.F. Chan, E. Gallopoulos, V. Simoncini, T. Szeto, C.H. Tong, "A Quasi-Minimal Residual Variant of the Bi-CGSTAB Algorithm for Nonsymmetric Systems", SIAM J. Sci. Statist. Comput., 15, 338-247, 1994.

13

C.C. Paige, M.A. Saunders, "LSQR: An Algorithm for Sparse Linear Equations and Sparse Least Squares", ACM Trans. Math. Soft., 8, 1, 43-71, 1982.

return to the contents page